Effective HamiltonianThe most general WIMP-nucleus interaction complying with Galilean symmetry can be parameterized with an effective Hamiltonian \(\mathcal{H}\) of the form, \[\mathcal{H}(w_i,q)=\sum_{\tau=0,1}\sum c^\tau_j (w_i,q) \mathcal{O}_j(q) t^\tau\] where \(w_i \) represents the Wilson coefficient, \(q\) the momentum transfer, and \(\mathcal{O}_j\) are respective interaction operators.In WimPyDD an Effective Hamiltonian can be initialized by instantiating the class eft_hamiltonian, which takes two arguments:
>>> hamiltonian=WD.eft_hamiltonian(string,wc) Input
func1, func2, ... are functions of the parameters \(w_i\), \(q\) that return the corresponding Wilson coefficients \(c^0,c^1\) in GeV\(^{-2}\) The Hamiltonian can be written either in the base of Anand et al, or in that of Gondolo et al Operator base of Anand et al,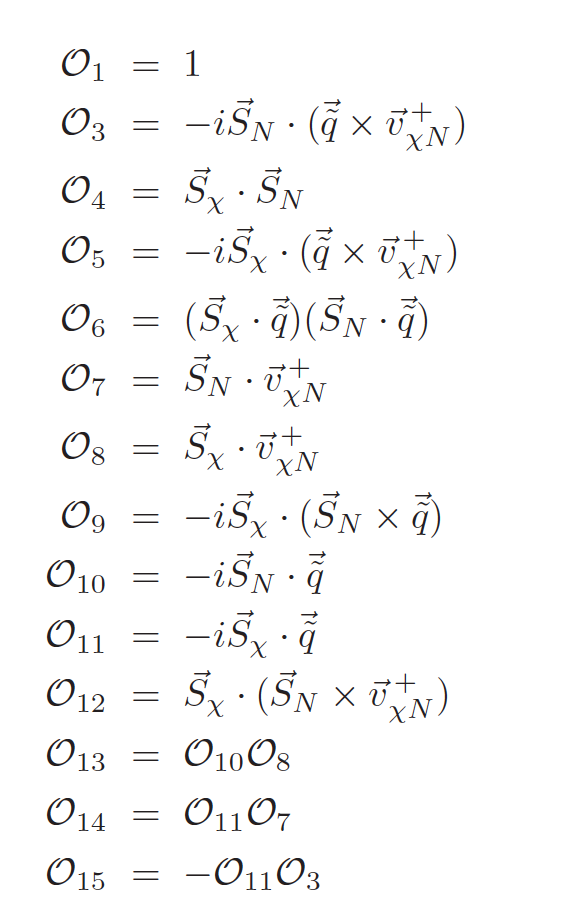
The keys n1, n2,...of the input dictionary must be integers picked by the list, [1,3,4,5,6,7,8,9,10,11,12,12,14,15] Operator base of Gondolo et al,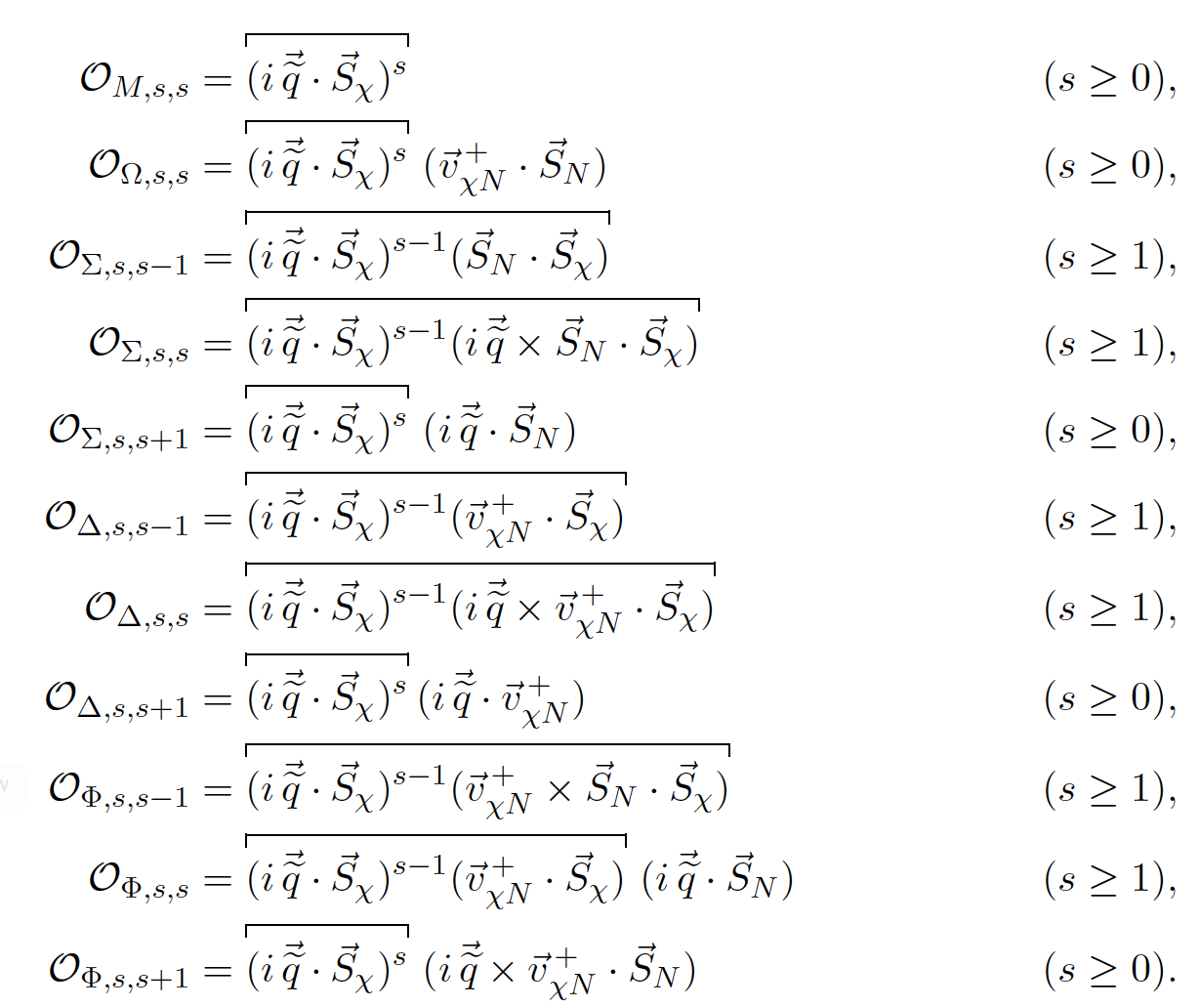
The keys n1,n2,...of the input dictionary must be tuples (X,s,l) with,
Example: Anapole Dark Matter S. Kang et. al, JCAP 1811(2018) no.11,040,
Defining the two functions c8_anapole(mchi,sigma_ref) and c9_anapole(mchi,sigma_ref) (see here for an example of their implementation) the Hamiltonian is given by:
>>> wc_anapole={8: c8_anapole, 9: c9_anapole}
>>> anapole=WD.eft_hamiltonian('anapole',wc_anapole)
>>> print(anapole) Hamiltonian name:anapole Hamiltonian:c8_anapole(mchi, sigma_ref)* O_8+c9_anapole(mchi, sigma_ref)* O_9 Squared amplitude contributions: O_8*O_8, O_8*O_9, O_9*O_9 so that: >>> wc_anapole_2={('Delta',1,0): c8_anapole, ('Sigma',1,1): c9_anapole}
>>> anapole_2=WD.eft_hamiltonian('anapole_2',wc_anapole_2)
>>> print(anapole_2) Hamiltonian name:anapole_2 Hamiltonian:c8_anapole(mchi, sigma_ref)* O_Delta_1_0
+c9_anapole(mchi, sigma_ref)* O_Sigma_1_1
Squared amplitude contributions: O_Delta_1_0*O_Delta_1_0, O_Delta_1_0*O_Sigma_1_1, O_Sigma_1_1*O_Sigma_1_1 leads to the same result. names of the files where the get_response_functions routine saves the response functions. For instance, >>> WD.load_response_functions(WD.XENON_1T_2018, anapole, j_chi=0.5) loads or saves the following files in the directory WimPyDD/Experiments/XENON_1T_2018/spin_1_2: c8_c8.npyWimPyDD/Experiments/XENON_1T_2018/spin_1_2: c8_c9.npy WimPyDD/Experiments/XENON_1T_2018/spin_1_2: c9_c9.npy for the WD.XENON_1T_2018 experiment (the 'XENON1T' folder name is determined by the XENON_1T_2018.name attribute). Analogously: >>> WD.load_response_functions(WD.XENON_1T_2018,anapole_2,j_chi=0.5) loads and/or saves: WimPyDD/Experiments/XENON_1T_2018/spin_1_2/c_Delta_1_0_c_Delta_1_0.npyWimPyDD/Experiments/XENON_1T_2018/spin_1_2/c_Delta_1_0_c_Sigma_1_1.npy WimPyDD/Experiments/XENON_1T_2018/spin_1_2/c_Sigma_1_1_c_Sigma_1_1.npy in the same directory. Different effective Hamiltonians can share the same set of response functions, if they have some effective operators in common. For instance, if \(a^{0}(r)=1+r\) and \(a^{1}(r)=1-r\) the Hamiltonian: \[{\cal H}(r,g,M) = \sum_{\tau=0,1} \left [\frac{g}{M^2}a^\tau(r) {\cal O}_8^\tau \right ]\] >>> H8=WD.eft_hamiltonian('H8',{8: lambda M,g,r=1: g/M**2*np.array([1+r,1-r])})
loads the tabulated response function from the same file c8_c8.npy used by anapole. However this is only possible if the Wilson coefficients do not depend on the transferred momentum, or they have the same momentum dependence, since the additional energy dependence contained in the Wilson coefficient requires the calculation of a different response function. As a consequence, in this case more control on where the response functions are saved is required. See here how to handle this case. Main attributes and methods of the eft_hamiltonian classFor the anapole and anapole_2 hamiltonians defined above: >>> [attr for attr in dir(anapole) if '__' not in attr] ['arguments', 'coeff_squared', 'coeff_squared_list', 'coeff_squared_q_dependence', 'couplings', 'default_args', 'global_arguments', 'global_default_args', 'hamiltonian', 'name', 'print_hamiltonian', 'print_hamiltonian_latex', 'wilson_coefficients'] >>> anapole.coeff_squared(8,9,mchi=100,sigma_ref=1e-40) array([[-6.68076649e-12, -3.57340160e-11], [-6.68076649e-12, -3.57340160e-11]]) Returns the 2\( \times \) 2 matrix \(c_8^{\tau}c_9^{\tau^{\prime}}\) as a function of the Hamiltonian parameters. The same output, i.e. the 2\( \times \) 2 matrix \(c_{\Delta,1,0}^{\tau}c_{\Sigma,1,1}^{\tau^{\prime}}\), is obtained by: >>> anapole_2.coeff_squared((('Delta',1,0)),('Sigma',1,1),mchi=100,sigma_ref=1e-40)
>>> anapole.coeff_squared_list [(8, 8), (8, 9), (9, 9)] >>> anapole_2.coeff_squared_list [(('Delta', 1, 0), ('Delta', 1, 0)), (('Delta', 1, 0), ('Sigma', 1, 1)),
(('Sigma', 1, 1), ('Sigma', 1, 1))]
Returns a list of the contributions \({\cal O}_j{\cal O}_k\) to the squared amplitude. >>> anapole.coeff_squared_q_dependence(0.1,8,9) Calculates the factorized momentum dependence of the product \(c_8^{\tau}c_9^{\tau^{\prime}}\). >>> anapole_2.coeff_squared_q_dependence(0.1,('Delta',1,0),('Sigma',1,1))
Calculates the same quantity for \(c_{\Delta,1,0}^{\tau}c_{\Sigma,1,1}^{\tau^{\prime}}\). Return 1 if the Wilson coefficients do not depend on \(q\). Depending on the interaction the Wilson coefficients have to be initialized. For example in the case of non-standard \(\mathcal{O}_5\) operatorWilson coefficients can be written as as: >>> wc={5 : lambda cp=1, cn=1, M=10**3: 1/M**2*np.array([cp+cn,cp-cn])}
Once the Wilson is defined user can write the EFT hamiltonian as: >>> c5=WD.eft_hamiltonian('c5', wc)
Here \(c_p\) and \(c_n\) are the WIMP couplings to proton and neutron respectively while \(M\) is any effective scale. As usual a short summary of effective_hamiltonian can be obtained by printing it: >>> print(c5) Hamiltonian name:c5 Hamiltonian:c_5(cp=1, cn=1, M=1000)* O_5 Squared amplitude contributions: O_5*O_5 In the case of more than one interactions the user can define the Wilson coefficients as following: >>> wc={8 : lambda cp=1, cn=1, q=1: 1/q**2*np.array([cp+cn,cp-cn]),
9 : lambda cp=1, cn=1: np.array([cp+cn,cp-cn])}) which leads to the following hamiltonian: >>> c8_c9=WD.eft_hamiltonian('c8_c9', wc)
As metioned before a short summary of EFT hamitonian can be obtained using print option: >>> print(c8_c9) Hamiltonian name:c8_c9 Hamiltonian:c_8(cp=1, cn=1, q=1)* O_8'(q)+c_9(cp=1, cn=1)* O_9 Squared amplitude contributions: O_8'(q)*O_8'(q), O_8'(q)*O_9, O_9*O_9 Notice that the operator \(\mathcal{O}_8\) depends on the transfer momentum (here a long range interaction) while \(\mathcal{O}_9\) is independent of that. A cautious user might have already noticed an interference term between \(\mathcal{O}_8\) and \(\mathcal{O}_9\) operators that is expected following EFT approach. The arguments of the defined Hamiltonian can be accessed by following: >>> c8_c9.arguments {8: ['cp', 'cn', 'q'], 9: ['cp', 'cn']}
If the value of an argument is not defined by the user it will be put to 1 by default. Notice that user should not pass the value of momentum transfer \(q\) in the argument as \(q\) is used in the calcualtion of the response functions and treated differently inside WimPyDD. But user has freedom to change any other arguments for example \(c_p, c_n\) here. Once the Nuclear Target and Effective Hamiltonian are defined, the user could move on to define an Experiment. |